Determining the inbreeding coefficient

Defining COI
In this course, we are using a special definition of inbreeding, using the context of COI:

Inbreeding coefficient of an individual is the probability that both alleles at a randomly taken locus of this individual are identical by descent.
Or in other words: the average homozygosity in an animal that is caused by ancestors common to both the sire and dam.

An animal inherits one copy of every gene from both its sire and dam.  There can be many different versions of a gene (these are called alleles), but each animal can have at most two.  If the pair of alleles in an animal are exactly the same version of the gene, that gene is "homozygous" (e.g., AA or aa); if the alleles are different, that gene is heterozygous (e.g., Aa).  If the sire and dam share a common ancestor, they might both have a copy of a particular allele that originated in that common ancestor, and therefore one of their offspring could inherit that same allele from both parents.

Let's look at a pedigree
Here is a standard 3 generation pedigree of a whippet born in 1972.  This has some inbreeding that originates in the third generation, specifically A Cappella's two grandmothers were full siblings (Golden Kate and Blue Kenzy); they were offspring of Happy Star Dickie x High Speeds Blue Kate.

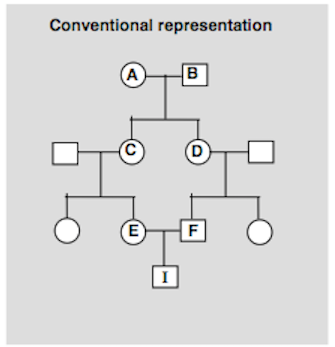
Let's explore the inbreeding in this pedigree.  First, we can simplify it by re-drawing this way:

Our dog A Cappella is at the bottom ("I"), the shared great-grandparents are at the top ("A" and "B"), and we can leave off the rest of the dogs.

We can see that if A has a copy of an allele for a particular gene (let's call it Ta), A could have passed it to C, then C to E, then E to A Cappella (I); similarly, A could have passed the Ta allele to D, who passed it to F, and then to A Capella.

If this happened, then A Cappella would be homozygous for the Ta allele.  In fact, we would say that A Cappella was "homozygous by descent" for that gene, which means that the two Ta alleles are not only identical, but they also originated from an ancestor that occurs on both the dam's and the sire's sides of the pedigree.  (A gene can also by "homozygous by state", which means the alleles are identical, but they did not originate from an ancestor that appears on both sides of the pedigree.)

We have described the paths an allele belonging to A could take to end up in A Cappella (I).  But there is another ancestor of A Cappella that is on both sides of the pedigree, which is B.  We could similarly trace the path an allele (let's say Tb) could take to get from B to A Cappella - B to D to F to I, and also B to C to E to I.

So we can see how an allele originating from one of the great grandparents (A or B) could show up in their descendant A Cappella.  And we can see how A Cappella might end up with two identical copies of that allele, one each from her two parents E and F, making her homozygous (and identical by descent) for that allele.

But how likely is this to happen?  We know that each gene in an animal has two alleles, which can be different or identical (e.g., TaTa, or TaTb; homozygous or heterozygous).  Which of the two alleles gets passed to the offspring is (theoretically) random, so in a litter of puppies, some will get Ta and some will get Tb if the parent is heterozygous.  Therefore, the probability of getting a particular allele is one chance in two, or 1/2 = 0.5, or 50%.

If we start with A, the probability of allele Tb being passed to offspring C is 50%.  Likewise, the chance of the Tb allele being passed from C to E is also 50%; and from E to I, also 50%.  We have a series of steps, each with a probability of 50%.  The probability that the Tb allele in A will be inherited through the series of ancestors C and E by the dog I is the product of the individual probabilities of each step, which are all 0.5.  And the allele Tb can be similarly passed on to I via the other side of the pedigree, through D and F.

 

 

Knowing that the probability of the allele moving from an ancestor to a descendent is 0.5, we can calculate the probability of moving from an ancestor through multiple descendants by multiplying the individual probabilities for each step.

So, for an allele to passed down the left branch of Path 1 from ancestor A to descendant I (above), we would calculate the probabilities like this:

for    A --> C,     p = 0.5 (or 50%)

for   A --> E,     p = 0.5 x 0.5 = 0.25 (or 25%)

for   A --> I,     p = 0.5 x 0.5 x 0.5 = 0.125 (or 12.5%)

Now, what do we do to determine the probability of I inheriting two copies of the same allele from ancestor A?  We need to consider the probabilities for each of the steps through the right branch of Path 1; i.e., A to D to F to I.

An easy way to do this calculation is by determining the number of ancestors in path starting from I (at the bottom) and counting each animal (node) to complete the loop through A and down the opposite side of the path.  So for Path 1 above starting at I, that would be

--> E --> C --> A --> D --> F

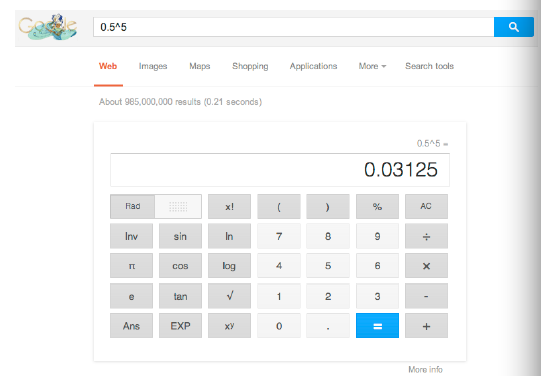
There are 5 animals in this complete path (from I back to I), and we know the probability of a particular allele being transmitted at each step is 0.5, so we can calculate the total probability as

 

---->  or,  F = 0.03125 (3.1%).

The "F" here is Wright's F - the Coefficient of Inbreeding (COI).

The calculation we just did indicated that there is just a 3% chance that I will be homozygous for an allele that originated in ancestor A.  Likewise, because of the inbreeding with A, about 3% of the genome of I will be homozygous.

So, for the next step, we have to consider both parents involved in this inbreeding, A and B in the first stick-figure pedigree diagram above.  The paths for B are just the same for A, so once again we have 5 animal nodes, and the F we would calculate due to inbreeding from B is once again 3.1%.

Now finally, we can compute the total probability of homozygosity in this breeding as

----->   F = 3.125% + 3.125% = 6.25%;

----->   therefore the COI of animal I is 6.25%.

Going back to the whippet pedigree above, the COI we would calculate for A Capella from the pedigree as we see it here is 6.25%.   This probability is exactly the same for a "good" gene (eg great temperament, coat color) as for a bad one (PRA, blue nose).  Which genes she will be homozygous for is a crap shoot; you can't breed for uniformity and predictability in some traits without also paying a penalty for increased homozygosity - and this, you'll recall from the first lesson, is the reason Wright derived the inbreeding coefficient in the first place. We won't gain a huge amount of homozygosity in the alleles we want if the coefficient of inbreeding is low (e.g., 6.25%), but then we are also keeping the level of risk relatively low - the probability of producing a dog that is homozygous for a gene we DON'T want is only 6.25%.  At COI of 6.25%, we accept a modest level benefit for a tolerably low level of risk.

This is a good place to stop so you can practice working out the paths in a few pedigrees and computing the inbreeding coefficients.  Things to remember - the focal animal (in these examples, individual I) - doesn't count as an animal in the loop.  Start with that animal and count the number of animals in a loop through the common ancestor and back again (call this "n"). Then calculate F (the coefficient of inbreeding) as 0.5 multiplied by 0.5 "n" times, or 0.5 raised to the power "n".  You don't need a fancy calculator to do this - let Google do the work!  Just type the formula into the Google search bar (use the "up" carrot ^ (shift 6) for the superscript, and Google will come back with a digital calculator with your answer.